鸢尾花书-矩阵力量

向量(Vector)

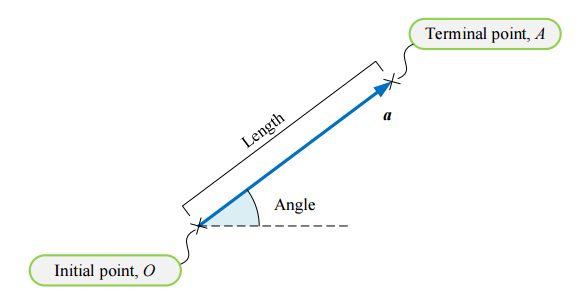
在平面上，向量是有方向的线段(directed line segment)。线段的长度代表向量的大小，箭头代表线段的方向。向量可以看成是特殊的矩阵——一维矩阵(one-dimensional matrix)。一行多列的向量是行向量(row vector)，一列多行的的向量是列向量(column vector)。

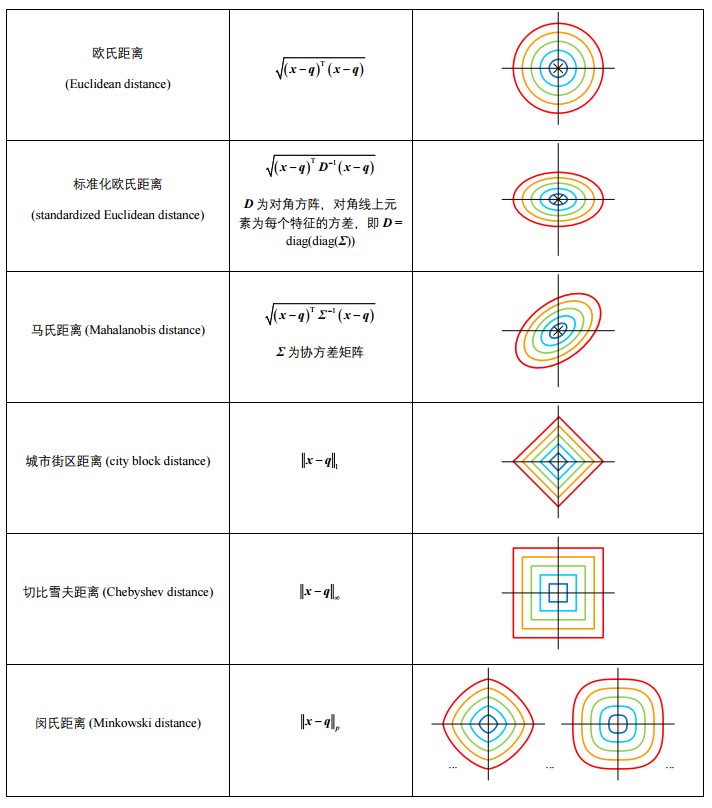
范数

对于给定列向量的范数定义如下：
$$
|\boldsymbol{x}|p=\left(\left|x_1\right|^p+\left|x_2\right|^p+\cdots+\left|x_D\right|^p\right)^{1 / p}=\left(\sum{j=1}^D\left|x_j\right|^p\right)^{1 / p}
$$

当时，不能称之为范数。
当时，向量的范数称为范数(L1-norm)。范数也叫城市街区距离(city block distance)，也称为曼哈顿距离(Manhattan distance)。具体定义为：

$$
|\boldsymbol{x}|1=\left|x_1\right|+\left|x_2\right|+\cdots+\left|x_D\right|=\sum{j=1}^D\left|x_j\right|
$$

当时，向量的范数称为范数(L2-norm)。范数也叫欧几里得距离(Euclidean distance))，也称为向量模长(vector norm)。具体定义为：

$$
|\boldsymbol{x}|2=\sqrt{x_1^2+x_2^2+\cdots x_D^2}=\left(\sum{j=1}^D x_j^2\right)^{\frac{1}{2}}
$$

当时，向量的范数称为范数。范数也叫切比雪夫距离(Chebyshev distance)。

把范数写成两个列向量和之差，常被称为查询点(query point)。
$$
|\boldsymbol{x}-\boldsymbol{q}|p=\left(\left|x_1-q_1\right|^p+\left|x_2-q_2\right|^p+\cdots+\left|x_D-q_D\right|^p\right)^{u_p}=\left(\sum{j=1}^D\left|x_j-q_j\right|^p\right)^{1 / p}
$$
范数作为空间中距离的度量，这个标量的大小代表距离的远近程度。不同的定义与平面直角坐标系中等距线如下图所示。

向量运算

向量内积(inner product)

向量内积又叫标量积(scalar product)，也称点积(dot product)。向量运算结果为标量，非矢量。

给定两个等行列向量

其内积定义如下：

常见性质如下：

从几何角度来看，向量内积相当于两个向量的模长与它们之间夹角余弦值的积：

向量和的内积为，称为正交(orthogonal)。余弦相似度(cosine similarity)使用向量夹角的余弦值来衡量样本数据的相似性，当余弦相似度为时，表明两个向量之间的夹角为，两个样本数据向量完全正相关；反之，余弦相似度为，表明两个样本数据完全反相关。余弦相似度为，表明两个样本数据无关。和两个向量的余弦相似度定义如下：

向量积(vector product)

向量积也叫叉乘(cross product)。向量运算结果为向量。向量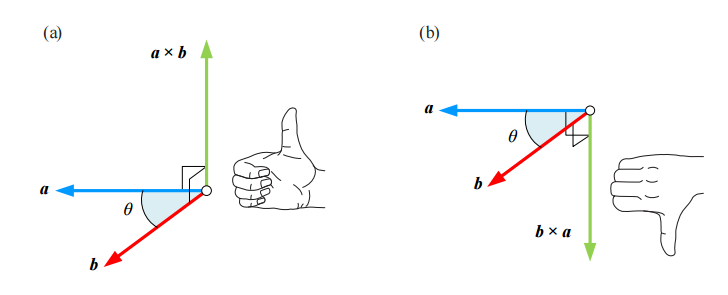和以及方向可以用右手定则判断。

常见的性质如下：

逐项积(piecewise product)

逐项积也称为阿达玛乘积(Hadamard product)。逐项积指两个形状相同的矩阵对于元素相乘得到同样形状大小的矩阵。对于两个列向量而言：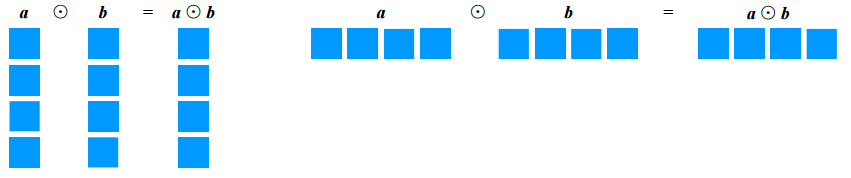

张量积(tensor product)

张量积又称克罗内克积(Kronecker product)。两个列向量的张量积为矩阵，相当于两个维度上的骨架张开一张网格面。当我们关注方向时, 网格面沿同一方向的每一条曲线都类似, 唯一的差别是高度上存在一定比例的缩放, 这个缩放比例就是。同理, 观察方向的网格面，每一条曲线都类似。向量的某一元素提供曲线高度的缩放系数。
$$
\boldsymbol{a} \otimes \boldsymbol{b}=\left[\right]{n \times 1} \otimes\left[\right]{m \times 1}=\boldsymbol{a} \boldsymbol{b}^{\mathrm{T}}=\left[\right]\left[\right]^{\mathrm{T}}=\left[\right]_{n \times m}
$$

常见的性质为：